度数の数え方をもっと楽に！【暗記しない音楽理論】

こんにちは、ふぅです。

以前から度数についての記事をまとめてきましたが、今回で3記事目です。

1記事目では、度数とは何かについて、

2記事目では、2つの音を入れ替えて音程を数えやすくする方法について紹介しました。

今回はもう一つ、度数を数えやすくする方法を紹介します。

分からなければ分かるところまでずらそう！

今回紹介する度数を数えやすくするテクニックは、「音程が分かるところまでずらして考える」というものです。

これだけ言われてもよく分からないと思うので、詳しく説明しますね。

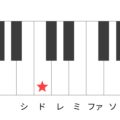
今回考えるのは、シとファ♯の音程です。

鍵盤だとこの位置ですね。

星印のついた二つの音の音程を考えます。

さて、みなさんは、シから始まる音程よりもドから始まる音程の方が数えやすいのではないのでしょうか？

そこで、シとファ♯の音程を、ドで始まる音程に直してみましょう。

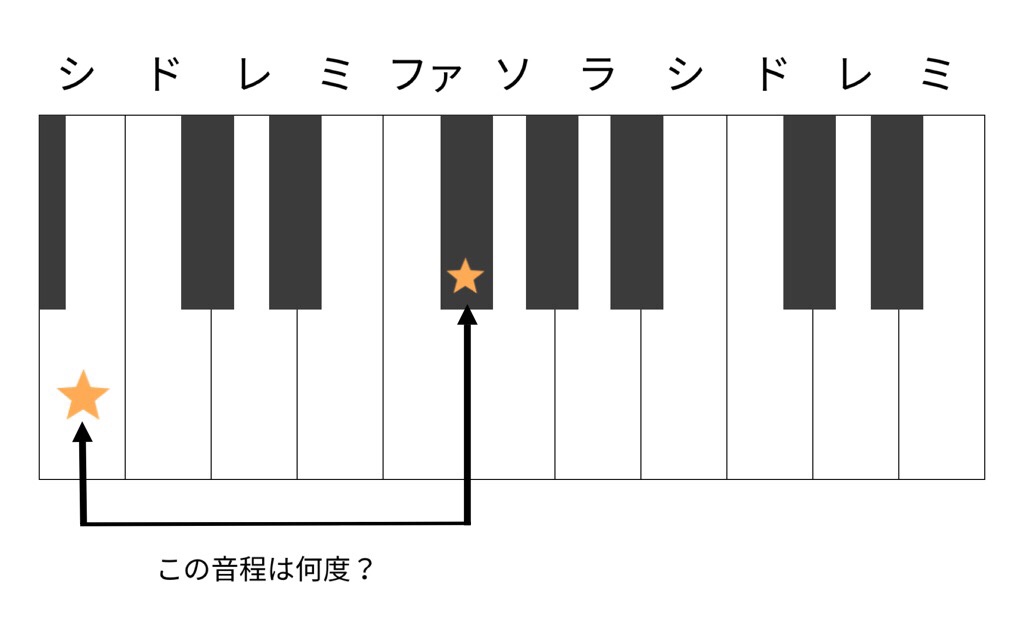
シは半音1つ分ずらすとドになります。同じようにファ♯も半音１つ分ずらしてあげると、ドで始まる音程になりますね。

2つの音が同じだけずれているので、音程は変わっていません。

ドとソの音程でしたら、もうお分かりですね。

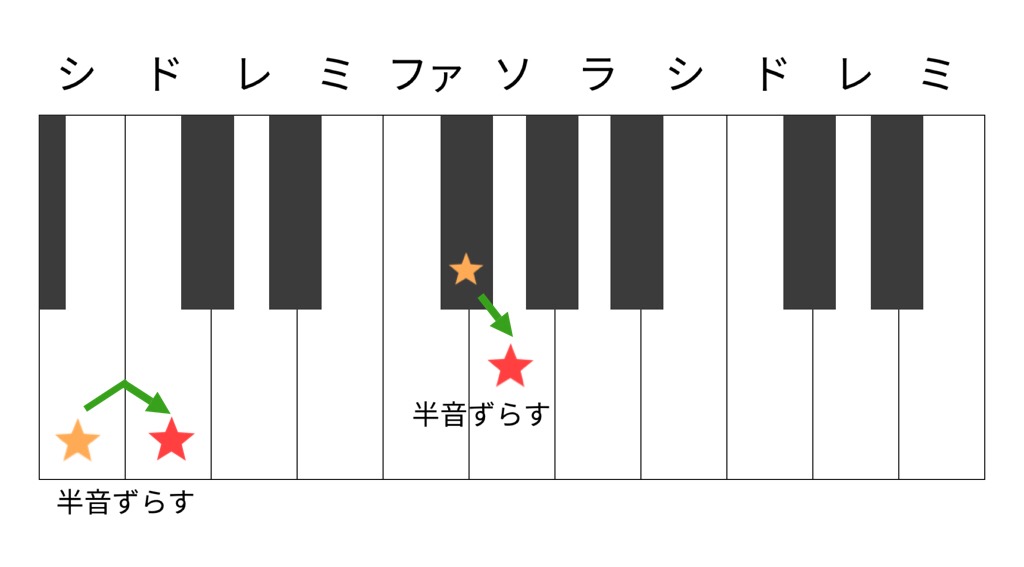
ド、レ、ミ、ファ、ソ…、とソはドで始まるメジャースケール上の5番目にくるので、完全5度です。

というわけで、シとファ♯の音程は、ドとソの音程と同じ完全5度だと分かりました。

鍵盤でいうと、赤の2つの星がドとソ、オレンジの2つの星がシとファ♯です。

同じ色の星同士では、間にある音の数が変わらないのに注目してください。

これじゃあミとシとかはどうするの？と思った方もいると思いますが、これは前回紹介した「音程を入れ替える」という方法と組み合わせると簡単に分かります。

次の章で詳しく説明しますね。

では、ミとシの音程を考えていきましょう。
手順をまとめると、

まず、2つの音を入れ替えて、シとミの音程を考えます。(手順1)

シからよりもドからの音程が数えやすいので、ドから始まる音程に直します。(手順2)

シは半音1つ分ずらすとドになるので、ミも半音1つ分ずらしてファにすると、ドから始まる音程になりますね。

ドとファの音程は完全4度なので、シとミの音程も完全4度です。

ここで分かるのは入れ替えた後の2つの音程(シとミ)であり、もとの音程(ミとシ)ではないことに注意してください。

では、シとミの音程をミとシの音程に直しましょう。(手順3)

詳しい説明は前回の記事で書いたので省きますが、

を使うと、ミとシの音程は完全5度だと分かります。

2回に渡って紹介した、度数を数えやすくする方法はいかがでしたか？

この方法を覚えれば、度数について覚えることも大分減るので、是非試してみてくださいね(^^)